原文地址：How we implemented consistent hashing efficiently

原文作者：Srushtika Neelakantam

译文出自：掘金翻译计划

本文永久链接：https://github.com/xitu/gold-miner/blob/master/TODO1/how-to-implement-consistent-hashing-efficiently.md

译者：yqian1991

校对者：Starrier

我们是如何高效实现一致性哈希的

Ably 的实时平台分布在超过 14 个物理数据中心和 100 多个节点上。为了保证负载和数据都能够均匀并且一致的分布到所有的节点上，我们采用了一致性哈希算法。

在这篇文章中，我们将会理解一致性哈希到底是怎么回事，为什么它是可伸缩的分布式系统架构中的一个重要工具。然后更进一步，我们会介绍可以用来高效率规模化实现一致性哈希算法的数据结构。最后，我们也会带大家看一看用这个算法实现的一个可工作实例。

再谈哈希

还记得大学里学的那个古老而原始的哈希方法吗？通过使用哈希函数，我们确保了计算机程序所需要的资源可以通过一种高效的方式存储在内存中，也确保了内存数据结构能被均匀加载。我们也确保了这种资源存储策略使信息检索变得更高效，从而让程序运行得更快。

经典的哈希方法用一个哈希函数来生成一个伪随机数，然后这个伪随机数被内存空间大小整除，从而将一个随机的数值标识转换成可用内存空间里的一个位置。就如同下面这个函数所示：

location = hash(key) mod size

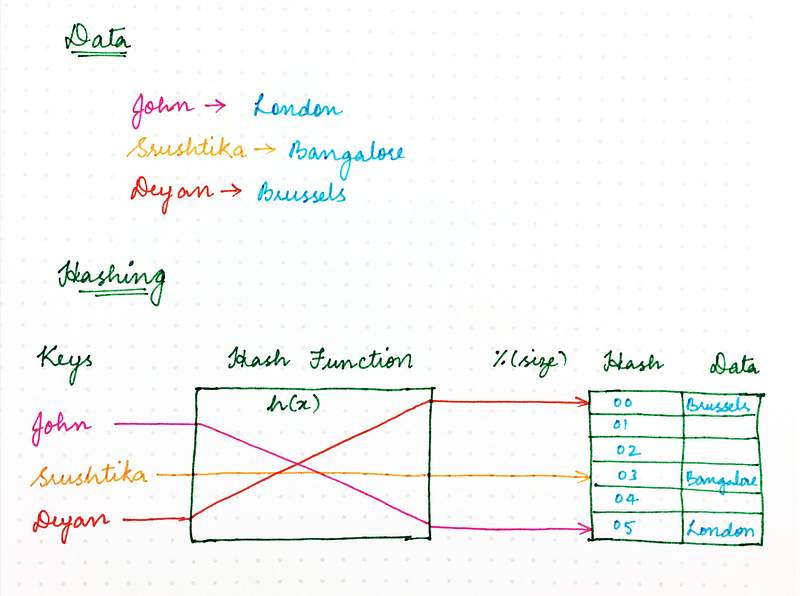
既然如此，我们为什么不能用同样的方法来处理网络请求呢？

在各种不同的程序、计算机或者用户从多个服务器请求资源的场景里，我们需要一种机制来将请求均匀地分布到可用的服务器上，从而保证负载均衡，并且保持稳定一致的性能。我们可以将这些服务器节点看做是一个或多个请求可以被映射到的位置。

现在让我们先退一步。在传统的哈希方法中，我们总是假设：

内存位置的数量是已知的，并且
这个数量从不改变

例如，在 Ably，我们一整天里通常需要扩大或者缩减集群的大小，而且我们也要处理一些意外的故障。但是，如果我们考虑前面提到的这些场景的话，我们就不能保证服务器数量是不变的。如果其中一个服务器发生意外故障了怎么办？如果继续使用最简单的哈希方法，结果就是我们需要对每个哈希键重新计算哈希值，因为新的映射完全决定于服务器节点或者内存地址的数量，如下图所示：

节点变化之前

节点变化之后

在分布式系统中使用简单再哈希存在的问题 — 每个哈希键的存放位置都会变化 — 就是因为每个节点都存放了一个状态；哪怕只是集群数目的一个非常小的变化，都可能导致需要重新排列集群上的所有数据，从而产生巨大的工作量。随着集群的增长，重新哈希的方法是没法持续使用的，因为重新哈希所需要的工作量会随着集群的大小而线性地增长。这就是一致性哈希的概念被引入的场景。

一致性哈希 — 它到底是什么？

一致性哈希可以用下面的方式描述：

它用虚拟环形的结构来表示资源请求者（为了叙述方便，后文将称之为“请求”）和服务器节点，这个环通常被称作一个 hashring。
存储位置的数量不再是确定的，但是我们认为这个环上有无穷多个点并且服务器节点可以被放置到环上的任意位置。当然，我们仍然可以使用哈希函数来选择这个随机数，但是之前的第二个步骤，也就是除以存储位置数量的那一步被省略了，因为存储位置的数量不再是一个有限的数值。
请求，例如用户，计算机或者无服务（serverless）程序，这些就等同于传统哈希方法中的键，也使用同样的哈希函数被放置到同样的环上。

那么它到底是如何决定请求被哪个服务器所服务呢？如果我们假设这个环是有序的，而且在环上进行顺时针遍历就对应着存储地址的增长顺序，每个请求可以被顺时针遍历过程中所遇到的第一个节点所服务；也就是说，第一个在环上的地址比请求的地址大的服务器会服务这个请求。如果请求的地址比节点中的最大地址还大，那它会反过来被拥有最小地址的那个服务器服务，因为在这个环上的遍历是以循环的方式进行的。方法用下图进行了阐明：

理论上，每个服务器‘拥有’哈希环（hashring）上的一段区间范围，任何映射到这个范围里的请求都将被同一个服务器服务。现在好了，如果其中一个服务器出现故障了怎么办，就以节点 3 为例吧，这个时候下一个服务器节点在环上的地址范围就会扩大，并且映射到这个范围的任何请求会被分派给新的服务器。仅此而已。只有对应到故障节点的区间范围内的哈希需要被重新分配，而哈希环上其余的部分和请求 - 服务器的分配仍然不会受到影响。这跟传统的哈希技术正好是相反的，在传统的哈希中，哈希表大小的变化会影响全部的映射。因为有了 一致性哈希，只有一部分（这跟环的分布因子有关）请求会受已知的哈希环变化的影响。（节点增加或者删除会导致环的变化，从而引起一些请求 - 服务器之间的映射发生改变。）

一种高效的实现方法

现在我们对什么是哈希环已经熟悉了…

我们需要实现以下内容来让它工作：

一个从哈希空间到集群上所有服务器节点之间的映射，让我们能找到可以服务指定请求的节点。
一个集群上每个节点所服务的请求的集合。在后面，这个集合可以让我们找到哪些哈希因为节点的增加或者删除而受到了影响。

映射

要完成上述的第一个部分，我们需要以下内容：

一个哈希函数，用来计算已知请求的标识（ID）在环上对应的位置。
一种方法，用来寻找转换为哈希值的请求标识所对应的节点。

为了找到与特定请求相对应的节点，我们可以用一种简单的数据结构来阐释，它由以下内容组成：

一个与环上的节点一一对应的哈希数组。
一张图（哈希表），用来寻找与已知请求相对应的服务器节点。

这实际上就是一个有序图的原始表示。

为了能在以上数据结构中找到可以服务于已知哈希值的节点，我们需要：

执行修改过的二分搜索，在数组中查找到第一个等于或者大于（≥）你要查询的哈希值所对应的节点 — 哈希映射。
查找在图中发现的节点 — 哈希映射所对应的那个节点。

节点的增加或者删除

在这篇文章的开头我们已经看到了，当一个节点被添加，哈希环上的一部分区间范围，以及它所包括的各种请求，都必须被分配到这个新节点。反过来，当一个节点被删除，过去被分配到这个节点的请求都将需要被其他节点处理。

如何寻找到被哈希环的改变所影响的那些请求？

一种解决方法就是遍历分配到一个节点的所有请求。对每个请求，我们判断它是否处在环发生变化的区间范围内，如果有需要的话，把它转移到其他地方。

然而，这么做所需要的工作量会随着节点上请求数量的增加而增加。让情况变得更糟糕的是，随着节点数量的增加，环上发生变化的数量也可能会增加。最坏的情况是，由于环的变化通常与局部故障有关，与环变化相关联的瞬时负载也可能增加其他受影响节点发生故障的可能性，有可能导致整个系统发生级联故障。

考虑到这个因素，我们希望请求的重定位做到尽可能高效。最理想的情况是，我们可以将所有请求保存在一种数据结构里，这样我们能找到环上任何地方发生哈希变化时受到影响的请求。

高效查找受影响的哈希值

在集群上增加或者删除一个节点将改变环上一部分请求的分配，我们称之为 受影响范围（affected range）。如果我们知道受影响范围的边界，我们就可以把请求转移到正确的位置。

为了寻找受影响范围的边界，我们从增加或者删除掉的一个节点的哈希值 H 开始，从 H 开始绕着环向后移动（图中的逆时针方向），直到找到另外一个节点。让我们将这个节点的哈希值定义为 S（作为开始）。从这个节点开始逆时针方向上的请求会被指定给它（S），因此它们不会受到影响。

注意：这只是实际将发生的情况的一个简化描述；在实践中，数据结构和算法都更加复杂，因为我们使用的复制因子（replication factors）数目大于 1，并且当任意给定的请求都只有一部分节点可用的情况下，我们还会使用专门的复制策略。

那些哈希值在被找到的节点和增加（或者删除）的节点范围之间的请求就是需要被移动的。

高效查找受影响范围内的请求

一种解决方法就是简单的遍历对应于一个节点的所有请求，并且更新那些哈希值映射到此范围内的请求。

在 JavaScript 中类似这样：

for (const request of requests) {
  if (contains(S, H, request.hash)) {
    /* 这个请求受环变化的影响 */
    request.relocate();
  }
}
function contains(lowerBound, upperBound, hash) {
   const wrapsOver = upperBound < lowerBound;
   const aboveLower = hash >= lowerBound;
   const belowUpper = upperBound >= hash;
   if (wrapsOver) {
     return aboveLower || belowUpper;
   } else {
     return aboveLower && belowUpper;
   }
}

由于哈希环是环状的，仅仅查找 S <= r < H 之间的请求是不够的，因为 S 可能比 H 大（表明这个区间范围包含了哈希环的最顶端的开始部分）。函数 contains() 可以处理这种情况。

只要请求数量相对较少，或者节点的增加或者删除的情况也相对较少出现，遍历一个给定节点的所有请求还是可行的。

然而，随着节点上的请求数量的增加，所需的工作量也随之增加，更糟糕的是，随着节点的增加，环变化也可能发生得更频繁，无论是因为在自动节点伸缩（automated scaling）或者是故障转换（failover）的情况下为了重新均衡访问请求而触发的整个系统上的并发负载。

最糟的情况是，与这些变化相关的负载可能增加其它节点发生故障的可能性，有可能导致整个系统范围的级联故障。

为了减轻这种影响，我们也可以将请求存储到类似于之前讨论过的一个单独的环状数据结构中，在这个环里，一个哈希值直接映射到这个哈希对应的请求。

这样我们就能通过以下步骤来定位受影响范围内的所有请求：

定位从 S 开始的第一个请求。
顺时针遍历直到你找到了这个范围以外的一个哈希值。
重新定位落在这个范围之内的请求。

当一个哈希更新时所需要遍历的请求数量平均是 R/N，R 是定位到这个节点范围内的请求数量，N 是环上哈希值的数量，这里我们假设请求是均匀分布的。

让我们通过一个可工作的例子将以上解释付诸实践：

假设我们有一个包含节点 A 和 B 的集群。

让我们随机的产生每个节点的 ‘哈希分配’：（假设是32位的哈希），因此我们得到了

A:0x5e6058e5

B:0xa2d65c0

在此我们将节点放到一个虚拟的环上，数值 0x0、0x1 和 0x2… 是被连续放置到环上的直到 0xffffffff，就这样在环上绕一个圈后 0xffffffff 的后面正好跟着的就是 0x0。

由于节点 A 的哈希是 0x5e6058e5，它负责的就是从 0xa2d65c0+1 到 0xffffffff，以及从 0x0 到 0x5e6058e5 范围里的任何请求，如下图所示：

另一方面，B 负责的是从 0x5e6058e5+1 到 0xa2d65c0 的范围。如此，整个哈希空间都被划分了。

从节点到它们的哈希之间的映射在整个集群上是共享的，这样保证了每次环计算的结果总是一致的。因此，任何节点在需要服务请求的时候都可以判断请求放在哪里。

比如我们需要寻找（或者创建）一个新的请求，这个请求的标识符是 ‘bobs.blog@example.com’。

我们计算这个标识的哈希 H ，比如得到的是 0x89e04a0a
我们在环上寻找拥有比 H 大的哈希值的第一个节点。这里我们找到了 B。

因此 B 是负责这个请求的节点。如果我们再次需要这个请求，我们将重复以上步骤并且又会得到同样的节点，它会包含我们需要的的状态。

这个例子是过于简单了。在实际情况中，只给每个节点一个哈希可能导致负载非常不均匀的分布。你可能已经注意到了，在这个例子中，B 负责环的 (0xa2d656c0-0x5e6058e5)/232 = 26.7%，同时 A 负责剩下的部分。理想的情况是，每个节点可以负责环上同等大小的一部分。

让分布更均衡合理的一种方法是为每个节点产生多个随机哈希，像下面这样：

事实上，我们发现这样做的结果照样令人不满意，因此我们将环分成 64 个同样大小的片段并且确保每个节点都会被放到每个片段中的某个位置；这个的细节就不是那么重要了。反正目的就是确保每个节点能负责环上同等大小的一部分，因此保证负载是均匀分布的。（为每个节点产生多个哈希的另一个优势就是哈希可以在环上逐渐的被增加或者删除，这样就避免了负载的突然间的变化。）

假设我们现在在环上增加一个新节点叫做 C，我们为 C 产生一个随机哈希值。

A:0x5e6058e5

B:0xa2d65c0

C:0xe12f751c

现在，0xa2d65c0 + 1 和 0xe12f751c （以前是属于A的部分）之间的环空间被分配给了 C。所有其他的请求像以前一样继续被哈希到同样的节点。为了处理节点职责的变化，这个范围内的已经分配给 A 的所有请求需要将它们的所有状态转移给 C。

现在你理解了为什么在分布式系统中均衡负载是需要哈希的。然而我们需要一致性哈希来确保在环发生任何变化的时候最小化集群上所需要的工作量。

另外，节点需要存在于环上的多个地方，这样可以从统计学的角度保证负载被均匀分布。每次环发生变化都遍历整个哈希环的效率是不高的，随着你的分布式系统的伸缩，有一种更高效的方法来决定什么发生了变化是很必要的，它能帮助你尽可能的最小化环变化带来的性能上的影响。我们需要新的索引和数据类型来解决这个问题。

构建分布式系统是很难的事情。但是我们热爱它并且我们喜欢谈论它。如果你需要依靠一种分布式系统的话，选择 Ably。如果你想跟我们谈一谈的话，联系我们！

在此特别感谢 Ably 的分布式系统工程师 John Diamond 对本文的贡献。

Srushtika 是 Ably Realtime的软件开发顾问

感谢 John Diamond 和 Matthew O’Riordan。

如果发现译文存在错误或其他需要改进的地方，欢迎到掘金翻译计划对译文进行修改并 PR，也可获得相应奖励积分。文章开头的 本文永久链接 即为本文在 GitHub 上的 MarkDown 链接。

掘金翻译计划是一个翻译优质互联网技术文章的社区，文章来源为掘金上的英文分享文章。内容覆盖 Android、iOS、前端、后端、区块链、产品、设计、人工智能等领域，想要查看更多优质译文请持续关注掘金翻译计划、官方微博、知乎专栏。